Aizu Online Judge(AOJ)が提供している「アルゴリズムとデータ構造入門」(ALDS1)の5_C問題をC++で解いてみました。
ALDS1では、「アルゴリズムとデータ構造の基礎を体得します。」とあります。トピック#5「分割統治法」では、部分的な小さな問題を解くことによって、与えられた元の問題を解く手法を紹介します。
問題(5_C: Koch Curve)
問題はリンク先をご覧ください。
再帰関数の応用としてコッホ曲線の座標を計算します。
コッホ曲線について
再帰関数を使って再帰的な構造を持つ図形の座標を計算します。
始点 p1、終了する点 p2 から、中間の点 s、u、t を求めます。以下は図は問題の一般解説から引用しました。
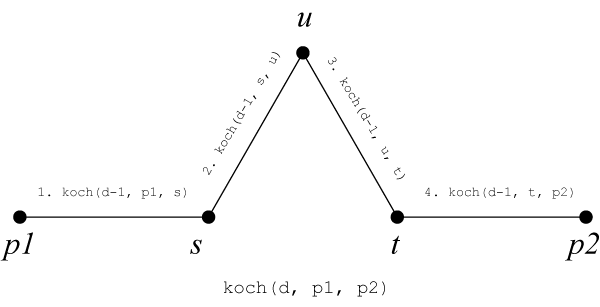
- 点 s は、点 p1 と点 p2 を繋いだ線分の3分の1の点となります。
- 点 t は、点 p1 と点 p2 を繋いだ線分の3分の2の点となります。
- 点 s を中心として点 t を 60 度回転させた点となります。回転行列を使って計算します。
上記で求めた s、u、 t を使って再帰的に以下のように呼び出します。
- 始点 p1、終了する点 s として再帰関数を呼び出す。
- 始点 s、終了する点 u として再帰関数を呼び出す。
- 始点 u、終了する点 t として再帰関数を呼び出す。
- 始点 t、終了する点 p2 として再帰関数を呼び出す。
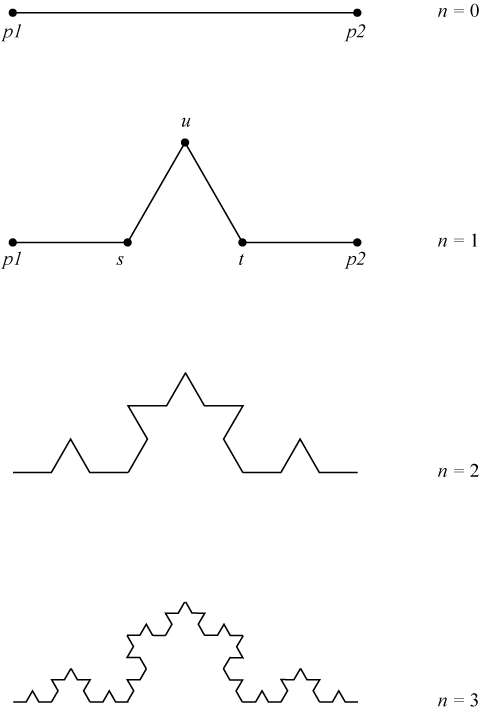
再帰的に呼び出すと以下の図(問題から引用)の座標が計算できます。
C++ プログラム例(ALDS1 5_C)
プログラムの補足です。
- 浮動小数点数を使うため、小数点以下の桁数の指定が楽な stdio を使いました。
- 二次元の点を表すクラス Point を定義しました(5ー9行目)。メソッド関数を定義していないため、struct で定義することもできますが、今後の拡張性を考慮しました。
- 再帰関数 koch は、上記解説のように実装しました。
以下が、最終的なC++プログラムとなります。
#include <cstdio>
#include <cmath>
using namespace std;
class Point {
public:
double x;
double y;
};
void koch(int n, Point p1, Point p2)
{
if (n == 0) {
return;
}
Point s, t, u;
double theta = M_PI * 60.0 / 180.0;
s.x = (2.0 * p1.x + 1.0 * p2.x) / 3.0;
s.y = (2.0 * p1.y + 1.0 * p2.y) / 3.0;
t.x = (1.0 * p1.x + 2.0 * p2.x) / 3.0;
t.y = (1.0 * p1.y + 2.0 * p2.y) / 3.0;
u.x = (t.x - s.x) * cos(theta) - (t.y - s.y) * sin(theta) + s.x;
u.y = (t.x - s.x) * sin(theta) + (t.y - s.y) * cos(theta) + s.y;
koch(n - 1, p1, s);
printf("%.6f %.6f\n", s.x, s.y);
koch(n - 1, s, u);
printf("%.6f %.6f\n", u.x, u.y);
koch(n - 1, u, t);
printf("%.6f %.6f\n", t.x, t.y);
koch(n - 1, t, p2);
}
int main()
{
int n;
scanf("%d", &n);
Point start = {0.0, 0.0};
Point end = {100.0, 0.0};
printf("%.6f %.6f\n", start.x, start.y);
koch(n, start, end);
printf("%.6f %.6f\n", end.x, end.y);
return 0;
}上記プログラムは、AOJ で「AC(Accepted=正解)」と判定されました。
最後に
高校で習う数学の知識を使いました。いままでほとんど図形の問題を解いていませんでしたが、よい学びになりました。
引き続き、ALDS1 の問題を紹介していきます。







