AtCoder が提供しているABC(AtCoder Beginner Contest)278 のE問題をC++で解いてみました。ABC278は、2022年11月19日21:00に実施されました。
AtCoder の紹介はこちらに、プログラミングの方針はこちらに記事があります。
E問題 Grid Filling(Difficulty : 996)
問題はリンク先をご覧ください。
二次元の累積和を計算しておいて、問題を解きます。AtCoder Problems による Difficulty は、996 でした。
解答案
問題の入力例1に掲載されている図を引用します。
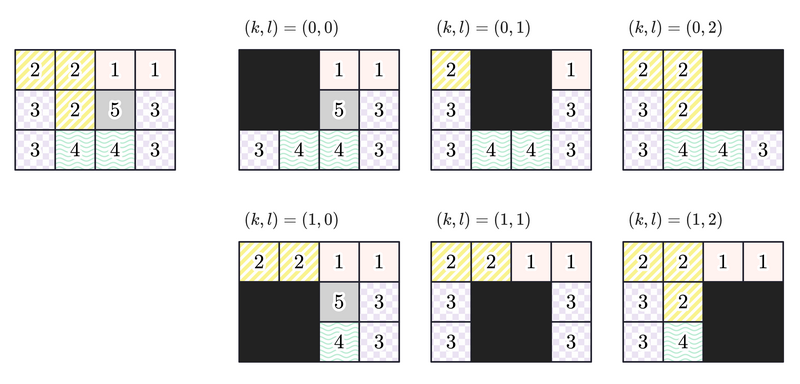
事前に、数字ごとに2次元累積和を計算しておきます。累積和を計算しておけば、数字ごとに黒で塗りつぶした範囲にある個数が $O(1)$ で分かります。黒で塗りつぶした範囲にすべての個数が入っていた場合、出力する数字を減らします。
C++ プログラム例(ABC278E)
プログラムの補足です。
- set コンテナ num に出現する数字を格納しておきます(13行目)。
- 出現する数字の2次元累積和を計算しておきます(17ー27行目)。
- それぞれの数字の塗りつぶす箱に含まれている個数を計算します(33ー37行目)。
- この問題に出現する数字の個数は、s[e][H][W]となるため、それと比較して、一致していれば、その数字はすべて塗りつぶされていないマスに表れないため、解答をひとつ減らします(38、39行目)。
以下が、C++プログラムとなります。
#include <bits/stdc++.h>
using namespace std;
int main()
{
int H, W, n, h, w;
cin >> H >> W >> n >> h >> w;
vector<vector<int>> a(H, vector<int>(W));
set<int> num;
for (int i = 0; i < H; ++i) {
for (int j = 0; j < W; ++j) {
cin >> a[i][j];
num.insert(a[i][j]);
}
}
vector<vector<vector<int>>> s(n + 1, vector<vector<int>>(H + 1, vector<int>(W + 1, 0)));
for (int i = 0; i < H; ++i) {
for (int j = 0; j < W; ++j) {
for (auto e : num) {
s[e][i + 1][j + 1] = s[e][i][j + 1];
s[e][i + 1][j + 1] += s[e][i + 1][j];
s[e][i + 1][j + 1] -= s[e][i][j];
s[e][i + 1][j + 1] += (a[i][j] == e);
}
}
}
for (int i = 0; i < H - h + 1; ++i) {
for (int j = 0; j < W - w + 1; ++j) {
int result = num.size();
for (auto e : num) {
int t = 0;
t += s[e][i + h][j + w];
t -= s[e][i][j + w];
t -= s[e][i + h][j];
t += s[e][i][j];
if (t == s[e][H][W]) {
--result;
}
}
cout << result << " \n"[j == W - w];
}
}
return 0;
}AC(Accepted=正しいプログラム)と判定されました。
Pythonは、多次元のリストが遅いのか、CPython 3.11.4 だけではなく、PyPy 3.10-v7.3.12 でも TLE でした。Python は、まだそれほど慣れておらずプログラムの紹介を断念します。
最後に
ABC331 D問題(解説記事)で2次元累積和を使いました。この問題も2次元累積和が使えるため、復習のつもりで解いてみました。
引き続き ABC の問題を紹介していきます。