Aizu Online Judge(AOJ)が提供している「アルゴリズムとデータ構造入門」(ALDS1)の7_A問題をC++で解いてみました。
ALDS1では、「アルゴリズムとデータ構造の基礎を体得します。」とあります。トピック#7「木構造」では、根付き木、二分木について紹介します。
問題(7_A: Rooted Trees)
問題はリンク先をご覧ください。
根付き木の構造について学びます。
木構造について(用語の整理)
入力例1の木構造を図示すると以下となります。
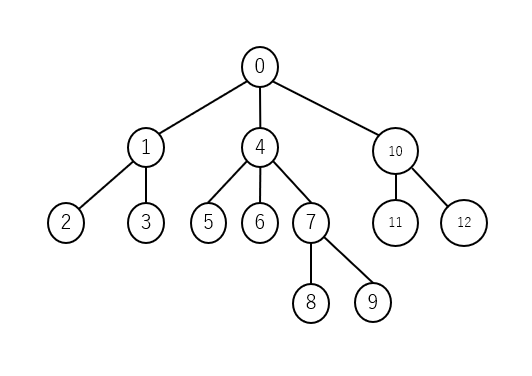
木構造の用語を整理します。図を用いて例示します。
- 根:その親がないグラフの頂点です。頂点0が根となります。
- 子:頂点0の子は、頂点1、4、10となります。
- 親:頂点1の親は頂点0、頂点8の親は頂点7となります。
- 葉:子がない頂点です。頂点2、3、5、6、8、9、11、12が葉になります。
- 内部節点:根でも葉でもない頂点です。頂点1、4、7、10が内部節点となります。
C++ プログラム例(ALDS1 7_A)
グラフとして処理します。
- 子として出てこない頂点が根になります。これはsetコンテナを用いて求めます。
- DFSを用いて、親(配列 parent)と深さ(配列 depth)を求めます。木を前提としているため、関数 dfs の実装は簡単になっています。
- 問題で示された出力をします。
- 入力例2の出力をみると、子の頂点はソートする必要はないようです。
以下が、C++プログラムとなります。
#include <iostream>
#include <vector>
#include <set>
#include <algorithm>
using namespace std;
vector<vector<int>> G;
vector<int> parent;
vector<int> depth;
void dfs(int v, int p, int d)
{
parent[v] = p;
depth[v] = d;
for (auto next_v : G[v]) {
dfs(next_v, v, d + 1);
}
}
int main()
{
int n;
cin >> n;
G.resize(n);
set<int> root;
for (int i = 0; i < n; ++i) {
root.insert(i);
}
for (int i = 0; i < n; ++i) {
int id;
int k;
cin >> id >> k;
for (int j = 0; j < k; ++j) {
int c;
cin >> c;
G[id].push_back(c);
root.erase(c);
}
}
parent.resize(n);
depth.resize(n);
int r = *(root.begin());
dfs(r, -1, 0);
for (int i = 0; i < n; ++i) {
cout << "node " << i << ": ";
cout << "parent = " << parent[i] << ", ";
cout << "depth = " << depth[i] << ", ";
if (i == r) {
cout << "root, ";
} else if (G[i].size() > 0) {
cout << "internal node, ";
} else {
cout << "leaf, ";
}
cout << "[";
for (int j = 0; j < G[i].size(); ++j) {
if (j != 0) {
cout << ", ";
}
cout << G[i][j];
}
cout << "]" << endl;
}
return 0;
}上記プログラムは、AOJ で「AC(Accepted=正解)」と判定されました。
最後に
トピック#7 では、木構造について学びます。
引き続き、ALDS1 の問題を紹介していきます。







