Aizu Online Judge(AOJ)が提供している「アルゴリズムとデータ構造入門」(ALDS1)の7_B問題をC++で解いてみました。
ALDS1では、「アルゴリズムとデータ構造の基礎を体得します。」とあります。トピック#7「木構造」では、根付き木、二分木について紹介します。
問題(7_B: Binary Trees)
問題はリンク先をご覧ください。
二分木の構造について学びます。
二分木について
入力例1の木構造を図示すると以下となります。この画像は、問題から引用させていただきました。
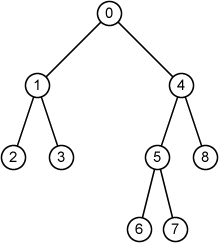
二分木は、左側の子と右側の子しか持ちません(持たない場合もある)。また、片方にしか子が無い場合に左側にある場合と右側にある場合を区別します。
C++ プログラム例(ALDS1 7_B)
7_A問題と比較した変化点のポイントは以下です。
- 二分木であるため、配列の配列ではなく、構造体の配列とすることができます。構造体のメンバは、parent(親)、left(左側の子)、right(右側の子)です。
- 関数 dfs の変化点
- 子は多くても2つしかないため、子の探索を条件文で記述する(一般のグラフでは、繰り返し文になる)。
- 木の高さは、左側の子の高さと右側の子の高さの高い方に1を加えた結果となる。
- 兄弟(sibling)の出力は、親に遡り自分ではない子を出力する。
以下が、C++プログラムとなります。
#include <iostream>
#include <vector>
#include <set>
#include <algorithm>
using namespace std;
typedef struct {
int parent;
int left;
int right;
} binary_tree;
vector<binary_tree> G;
vector<int> depth;
vector<int> height;
int dfs(int v, int d)
{
depth[v] = d;
int left_height = 0;
if (G[v].left != -1) {
left_height = dfs(G[v].left, d + 1) + 1;
}
int right_height = 0;
if (G[v].right != -1) {
right_height = dfs(G[v].right, d + 1) + 1;
}
height[v] = max(left_height, right_height);
return height[v];
}
int main()
{
int n;
cin >> n;
G.resize(n);
set<int> root;
for (int i = 0; i < n; ++i) {
root.insert(i);
}
for (int i = 0; i < n; ++i) {
int id, left, right;
cin >> id >> left >> right;
G[id].left = left;
if (left != -1) {
G[left].parent = id;
root.erase(left);
}
G[id].right = right;
if (right != -1) {
G[right].parent = id;
root.erase(right);
}
}
depth.resize(n);
height.resize(n);
int r = *(root.begin());
G[r].parent = -1;
height[r] = dfs(r, 0);
for (int i = 0; i < n; ++i) {
cout << "node " << i << ": ";
cout << "parent = " << G[i].parent << ", ";
if (G[i].parent == -1) {
cout << "sibling = " << -1 << ", ";
} else if (G[G[i].parent].left == i) {
cout << "sibling = " << G[G[i].parent].right << ", ";
} else {
cout << "sibling = " << G[G[i].parent].left << ", ";
}
int degree = 0;
if (G[i].left != -1) {
++degree;
}
if (G[i].right != -1) {
++degree;
}
cout << "degree = " << degree << ", ";
cout << "depth = " << depth[i] << ", ";
cout << "height = " << height[i] << ", ";
if (i == r) {
cout << "root";
} else if ((G[i].left != -1)||(G[i].right != -1)) {
cout << "internal node";
} else {
cout << "leaf";
}
cout << endl;
}
return 0;
}上記プログラムは、AOJ で「AC(Accepted=正解)」と判定されました。
最後に
二分木は、木構造としてはサブセットと考えることができます。このため、コンテナが簡単になるなど、実装も分かりやすくなっています。
引き続き、ALDS1 の問題を紹介していきます。







