ABC349 D問題（Divide Interval）を解く

AtCoder が提供しているABC（AtCoder Beginner Contest）349 のD問題をC++で解いてみました。ABC349は、2024年4月13日21:00に実施されました。

AtCoder の紹介はこちらに、プログラミングの方針はこちらに記事があります。

D問題 Divide Interval（Difficulty : 832）

問題はリンク先をご覧ください。

ABC349 D問題 Divide Interval

いくつかの解き方がありますが定義に従って演算します。AtCoder Problems による Difficulty は 832 でした。

解答案

入力例1について確認します。$L=3, R=19$ です。

• 左が3になる良い数列は、[3, 4) の1組しかありません。
  • $2^0 \times 3=3, 2^0 \times 4=4$
• 次に左が4になる良い数列は、[4, 5)、[4, 6)、[4, 8) の3組があります。
  • $2^0 \times 4=4, 2^0 \times 5=5$
  • $2^1 \times 2=4, 2^1 \times 3=6$
  • $2^2 \times 1=4, 2^2 \times 2=8$
• 次に左が8になる良い数列は、[8, 9)、[8, 10)、[8, 12)、[8, 16) の4組があります。
  • $2^0 \times 8=8, 2^0 \times 9=9$
  • $2^1 \times 4=8, 2^1 \times 5=10$
  • $2^2 \times 2=8, 2^2 \times 3=12$
  • $2^3 \times 1=8, 2^3 \times 2=16$
• 次に左が16になる良い数列は、[16, 17)、[16, 18) の2組があります。
  • $2^0 \times 16=16, 2^0 \times 17=17$
  • $2^1 \times 8=16, 2^1 \times 9=18$
  • $2^2 \times 4=16, 2^2 \times 5=20$、19を超えています。
  • $2^3 \times 2=16, 2^3 \times 3=24$、19を超えています。
  • $2^4 \times 1=16, 2^4 \times 2=32$、19を超えています。
• 次に左が18になる良い数列は、[18, 19) の1組しかありません。
  • $2^0 \times 18=18, 2^0 \times 19=19$
  • $2^1 \times 9=18, 2^1 \times 10=20$、19を超えています。

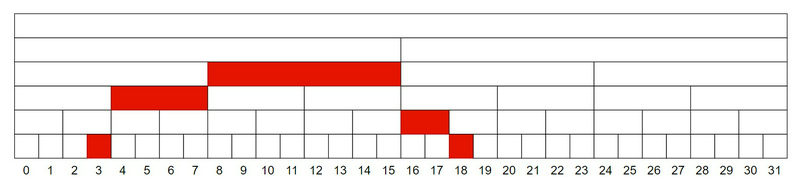
結果的に、貪欲にできるだけ右の大きい数字を取ればよいことが分かります。これが分割の個数を最小にする方法であることは、セグメント木の構造と同じになることから直感的に理解できます。

問題の分割をセグメント木として示した図です（この図は、公式解説から引用させていただきました）。

C++ プログラム例（ABC349D）

左側の値を2で割りながら、対応する右側の値を求めます。

• 左の値を仮に tL とします。初期値は、L とします。
• 対応する右の値を tR とします。初期値は、L+1 とします。
  • $2^0 \times L=L, 2^0 \times (L + 1) = L + 1$ となるため、右側の値の候補となります。
• 2で割りながら、変数 p2 を2倍していきます。p2 の初期値は1です。
  • (tL + 1) × p2 が右側の値の候補となります。
    入力例1で示した数式からこの式になることが分かります。
• R を超えない、最大値 tR を求めます。
• tR の値を、次のLとして扱います。

以下が、C＋＋プログラムとなります。

#include <bits/stdc++.h>
using namespace std;

typedef unsigned long long int ull;

int main()
{
	ull L, R;
	cin >> L >> R;

	vector<pair<ull, ull>> result;
	while (1) {
		ull tL = L;
		ull tR = L + 1;
		ull p2 = 1;
		while (tL % 2 == 0) {
			tL /= 2;
			p2 *= 2;
			if ((tL + 1) * p2 <= R) {
				tR = max(tR, (tL + 1) * p2);
			} else {
				break;
			}
		}
		if ((tL + 1) * p2 <= R) {
			tR = max(tR, (tL + 1) * p2);
		}
		result.push_back(make_pair(L, tR));
		L = tR;
		if (tR == R) {
			break;
		}
	}

	cout << result.size() << endl;
	for (int i = 0; i < result.size(); ++i) {
		cout << result[i].first << " " << result[i].second << endl;
	}

	return 0;
}

AC（Accepted＝正しいプログラム）と判定されました。

Python プログラム例（ABC349D）

Python 版も基本的な考え方は同じです。以下となります。

"""AtCoder Beginner Contest 349 D"""
L, R = map(int, input().split())

result = []
while True:
    tL = L
    tR = L + 1
    p2 = 1
    while tL % 2 == 0:
        tL //= 2
        p2 *= 2
        if (tL + 1) * p2 <= R:
            tR = max(tR, (tL + 1) * p2)
        else:
            break
    if (tL + 1) * p2 <= R:
        tR = max(tR, (tL + 1) * p2)
    result.append((L, tR))
    L = tR
    if tR == R:
        break

print(len(result))
for e in result:
    print(e[0], e[1])

こちらも「AC」と判定されました。

最後に

この問題は、残念ながらコンテスト中に解くことができませんでした。いくつかの方法で解くことができましたが、自分にとって一番理解しやすい方法を紹介しました。

引き続き ABC の問題を紹介していきます。