AtCoder が提供しているABC(AtCoder Beginner Contest)338 のD問題をC++とPythonで解いてみました。ABC338は、2024年1月27日21:00に実施されました。
AtCoder の紹介はこちらに、プログラミングの方針はこちらに記事があります。
D問題 Island Tour(Difficulty : 1234)
問題はリンク先をご覧ください。
短い経路が使えなくなった場合のペナルティをその径路に累積値として加えます。AtCoder Problems による Difficulty は 1234 でした。
解答案
$X_i$ から $X_{i+1}$ の経路が二つあります。入力例1を見てみましょう。以下の図は問題から引用させていただきました。
1→3→2 の経路の場合、橋1を壊しても最短経路に影響がないことが分かります(図の一番左)。
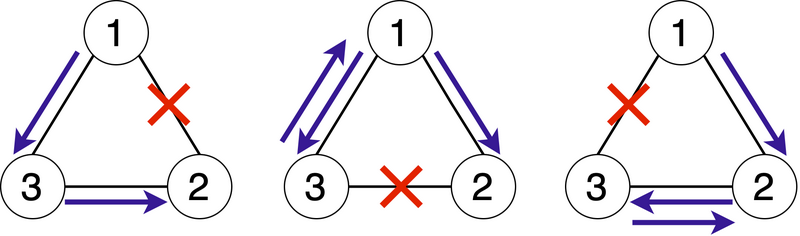
1→3と3→2を個別に考えます。
- 経路1→3について
- 1→3 と通れば長さ1
- 1→2→3 と通れば長さ2
- つまり橋3(1→3を通る経路にある橋)を壊せば、2-1 = 1 だけ不利になることが分かります。ペナルティ[橋3] = 1 と考えます。
- 経路3→2について
- 3→2 と通れば長さ1
- 3→1→2 と通れば長さ2
- つまり橋2(3→2を通る経路にある橋)を壊せば、2 – 1 = 1 だけ不利になることが分かります。ペナルティ[橋2] = 1 と考えます。
橋2と橋3を壊すとペナルティ1(最短距離が1増える)となることは上の図からも読み取れます。逆に橋1にはペナルティがなく、この橋を壊せば最短距離2から増えることなくツアーを終えることができます。
この考え方をまとめます。
- $X_i$ から $X_{i+1}$ に移動する短い経路と長い経路を求めます。
- 長い経路と短い経路の長さの差を短い経路のそれぞれの橋にペナルティとして加えます。
- ペナルティの合計が最も少ない橋を壊すことにします。
- ペナルティの合計がもっとも少ない橋のペナルティ合計にツアーの最短経路を加えた値が求める解答となります。
ペナルティを複数の橋に対して個別に加えると、計算時間が足りません。起点にプラス分を、終点+1の点にそれを相殺するマイナス分を加えて、後でまとめて加えるという方法を使うことによって、計算時間が間に合います。これは、いもす法と呼ばれています。
C++ プログラム例(ABC338D)
プログラムの補足です。
- a→bとb→aの経路の長さは変わらないため、a<bとなるようにします。二つの経路の長さ b-a と a+n-b の短い値が最短経路の長さとなります。
- 起点にペナルティ(長い値と短い値の差)を加えます。終点+1 に同じペナルティを引いて相殺します。橋N をまたぐ場合は、N+1 の点で相殺して、橋1 にペナルティを加えて計算します(35ー38行目)。
- このときに最短経路の長さの和 result も更新しておきます。
- 差分として表現したペナルティの値を累計して、ペナルティの合計を求めます。ペナルティの最小値を min_s として記憶します(42ー46行目)。
- 最後に result と min_s を加えた値を出力します。
以下が、C++プログラムとなります。
#include <bits/stdc++.h>
using namespace std;
typedef long long int ll;
#define INF (1LL << 60)
int main()
{
int n, m;
cin >> n >> m;
vector<int> x(m);
for (int i = 0; i < m; ++i) {
cin >> x[i];
}
ll result = 0;
vector<ll> s(n + 2, 0);
for (int i = 0; i < m - 1; ++i) {
ll pass1, pass2, diff;
ll from = x[i];
ll to = x[i + 1];
if (from > to) {
swap(from, to);
}
pass1 = to - from;
pass2 = from + n - to;
if (pass1 <= pass2) {
result += pass1;
diff = pass2 - pass1;
s[from] += diff;
s[to] -= diff;
} else {
result += pass2;
diff = pass1 - pass2;
s[to] += diff;
s[n + 1] -= diff;
s[1] += diff;
s[from] -= diff;
}
}
ll min_s = s[1];
for (int i = 1; i < n; ++i) {
s[i + 1] += s[i];
min_s = min(min_s, s[i + 1]);
}
cout << result + min_s << endl;
return 0;
}AC(Accepted=正しいプログラム)と判定されました。
Python プログラム例(ABC338D)
Python 版も基本的な考え方は同じです。以下となります。
"""AtCoder Beginner Contest 338 D"""
n, m = map(int, input().split())
x = list(map(int, input().split()))
result = 0
s = [0] * (n + 2)
for i in range(m - 1):
fr = x[i]
to = x[i + 1]
if fr > to:
fr, to = to, fr
pass1 = to - fr
pass2 = fr + n - to
if pass1 <= pass2:
result += pass1
diff = pass2 - pass1
s[fr] += diff
s[to] -= diff
else:
result += pass2
diff = pass1 - pass2
s[to] += diff
s[n + 1] -= diff
s[1] += diff
s[fr] -= diff
min_s = s[1]
for i in range(1, n):
s[i + 1] += s[i]
min_s = min(min_s, s[i + 1])
print(result + min_s)こちらも「AC」と判定されました。
最後に
コンテスト中には解くことができませんでした。公式解説の解き方が、自分で理解(腹落ち)するために時間がかかりました。時間はかかりましたが、自分なりの理解ができたため記事にしました。
引き続き ABC の問題を紹介していきます。