AtCoder が提供しているABC(AtCoder Beginner Contest)331 のD問題をC++とPythonで解いてみました。ABC331は、2023年12月2日21:00に実施されました。
AtCoder の紹介はこちらに、プログラミングの方針はこちらに記事があります。
D問題 Tile Pattern(Difficulty : 1361)
問題はリンク先をご覧ください。
2次元累積和を使います。AtCoder Problems による Difficulty は 1361 でした。
解答案
復習)1次元の累積和
問題に使う2次元の累積和の前に、1次元の累積和についてまとめます。
配列 a[i] (i = 0, … , n – 1) が与えられています。累積和となる配列 s (i = 0, … , n) を以下のコードで事前に計算しておきます。
vector<int> s(n + 1);
s[0] = 0;
for (int i = 0; i < n; ++i) {
s[i + 1] = s[i] + a[i];
}添え字の範囲 [left , right) の a[i] の和は、s[right] – s[left] で求めることができます。なお、累積和の添え字は、半開区間で考えると、1個違いミスを減らすことができます。
2次元の累積和
2次元の配列 a[i][j] が与えられています。同じように累積和となる配列 s を以下のコードで事前に計算しておきます。
vector<vector<int>> s(n + 1, vector<int>(n + 1, 0);
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
s[i + 1][j + 1] = s[i][j + 1] + s[i + 1][j] - s[i][j] + a[i][j];
}
}配列 s を使うと、[i1, i2) × [j1, j2) の範囲にある a[i][j] (i1 ≦ i < i2、j1 ≦ j < j2) の和は、以下となります。
s[i2][j2] – s[i1][j2] – s[i2][j1] + s[i1][j1]
s[i1][j1] を2回引いている分を加えて戻しているわけです。特に i1 = 0、j1 = 0 の場合、s[0][j2]、s[i2][0]、s[0][0] がすべて 0 になるため、s[i2][j2] と等しくなります。
後は、右下の座標 [0, i) × [0, j) に含まれる黒マスの個数を繰り返しパターンから求めるだけです。これはプログラムのところで解説します。
C++ プログラム例(ABC331D)
公式解説で以下の図が紹介されています。縦8マス、横7マスの中身を3×3のパターンで埋めています(この図も引用させていただきました)。
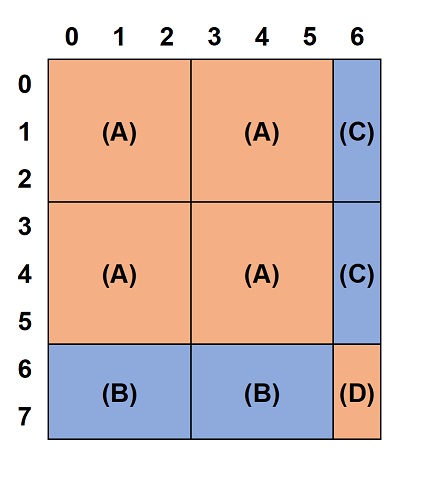
もし、繰り返すパターンに含まれる黒マスが s[3+1][3+1] として計算されていれば、
- (A) s[3][3](パターン分すべて)は、4個分含まれている。
- (B) 8 % 3 = 2 となり、s[2][3] は、2個分含まれている。
- (C) 7 % 3 = 1 となり、s[3][1] は、2個分含まれている。
- (D) 残りは、s[2][1] の個数となる。
縦 i、横 j に対して、[0, i) × [0, j) に含まれる黒マスの数を返す関数 black の詳細は、9ー25行目となります。上記の(A)から(D)に含まれる黒マスの個数を累積和 s から求めています。
本体処理の関数 main の補足です。
- 繰り返しパターンに含まれる黒マスの数を2次元の累積和 s として求めておきます(40ー44行目)。
- 読み込んだ a、b、c、d に対して、半開区間にするために c と d の値をインクリメントします。
- [a, c) × [b, d) に含まれる黒マスの数を関数 black を呼び出し求めます(51行目)。
以下が、C++プログラムとなります。
#include <bits/stdc++.h>
using namespace std;
typedef long long int ll;
int n;
vector<vector<int>> s;
ll black(int i, int j)
{
ll result = 0;
ll all = s[n][n];
ll ni = i / n;
ll nj = j / n;
result += all * ni * nj;
ll mi = i % n;
ll mj = j % n;
result += s[mi][mj];
result += s[mi][n] * nj;
result += s[n][mj] * ni;
return result;
}
int main()
{
int q;
cin >> n >> q;
vector<string> p(n);
for (int i = 0; i < n; ++i) {
cin >> p[i];
}
s.resize(n + 1);
for (int i = 0; i <= n; ++i) {
s[i].resize(n + 1, 0);
}
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
s[i + 1][j + 1] = s[i][j + 1] + s[i + 1][j] - s[i][j] + (p[i][j] == 'B');
}
}
for (int i = 0; i < q; ++i) {
int a, b, c, d;
cin >> a >> b >> c >> d;
++c;
++d;
cout << black(c, d) - black(a, d) - black(c, b) + black(a, b) << endl;
}
return 0;
}AC(Accepted=正しいプログラム)と判定されました。
Python プログラム例(ABC331D)
Python 版も基本的な考え方は同じです。以下となります。
"""AtCoder Beginner Contest 331 D"""
def black(i, j):
global n, s
result = 0
all_b = s[n][n]
ni = i // n
nj = j // n
result += all_b * ni * nj
mi = i % n
mj = j % n
result += s[mi][mj]
result += s[mi][n] * nj
result += s[n][mj] * ni
return result
n, q = map(int, input().split())
p = [input() for _ in range(n)]
s = [[0 for _ in range(n + 1)] for _ in range(n + 1)]
for i in range(n):
for j in range(n):
s[i + 1][j + 1] = s[i][j + 1] + s[i + 1][j] - s[i][j] \
+ (1 if p[i][j] == 'B' else 0)
for _ in range(q):
a, b, c, d = map(int, input().split())
c += 1
d += 1
print(black(c, d) - black(a, d) - black(c, b) + black(a, b))こちらも「AC」と判定されました。
最後に
2次元累積和についての知識はありましたが、コンテスト中は解くことができませんでした。公式解説を読み、頭を整理してプログラムを書きました。次に見たときに解けるようになればと思います。
引き続き ABC の問題を紹介していきます。