AtCoder が提供しているABC(AtCoder Beginner Contest)321 のE問題をC++とPythonで解いてみました。ABC321は、2023年9月23日21:00に実施されました。
AtCoder の紹介はこちらに、プログラミングの方針はこちらに記事があります。
E問題 Complete Binary Tree(Difficulty : 1627)
問題はリンク先をご覧ください。
ABC321 E問題 Complete Binary Tree
指定された頂点の子供と親を分けて条件を満たす頂点数を求めます。AtCoder Problems による Difficulty は 1627 でした。
解答案
$N = 10$ のとき、木は以下となります。この図は問題から引用しました。
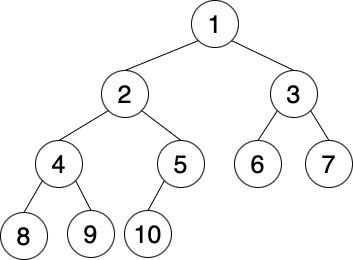
入力例1では、頂点 $X=2$ に注目しています。頂点の個数を子供側と親側に分けて考えます。
- 子供側:
- 距離が0の頂点は、2の1個となります。
- 距離が1の頂点は、4と5の2個となります。
- 距離が2の頂点は、8と9と10の3個となります。11も候補ですが、$N = 10$ より大きいため該当しません。
- 距離が3の頂点は、存在しません。
- 距離が $K$ の頂点は、以下となります。
- $X \times 2^k$ から $2^k$ 個の頂点かつ番号が $N$ 以下の頂点となります。
- $10^{18} \doteqdot 2^{60}$ となるため、計算量のループは、最大で60回程度発生します。
- 親側:
- 距離が1の頂点は、1の1個となります。
- 距離が2の頂点は、1から距離が1の子供の3の1個となります。
- 距離が3の頂点は、1から距離が2の子供の6と7の2異なります。
- 距離が4の頂点は、存在しません。
- 距離が $K$ の頂点数は、以下の和となります。
- X につながる経路以外の子供以降の頂点数をカウントして加える。
- 頂点1以外であれば、その親経由の頂点数を再帰的にカウントして加える。
- 最悪でも頂点1を経由して、末端まで調べるため、最大で60回の再帰と再帰毎に最大60回のループが発生します。
この考え方で子供側と親側の頂点数を求めて加えた値を出力します。
C++ プログラム例(ABC321E)
考え方は上記の通りですが、以下の場合も考慮します。
- 子供側(関数 down として実装):
- 距離が負の場合は、値を増やさない(0を返す)。
- 距離が0の場合は、指定された頂点番号が$N$以下なら1を返す。超えていれば0を返す。
- 親側(関数 up として実装):
- 距離が負、もしくは指定された頂点が1未満(存在しない)の場合は、値を増やさない(0を返す)。
- 距離が0の場合は、指定された頂点番号が$N$以下なら1を返す。超えていれば0を返す。
最終的に以下が、C++プログラムとなります。
#include <bits/stdc++.h>
using namespace std;
typedef long long int ll;
ll n;
ll down(ll dist, ll v)
{
if (dist < 0) {
return 0;
}
if (dist == 0) {
if (v <= n) {
return 1;
} else {
return 0;
}
}
ll next_v = v;
ll p = 1;
while (dist > 0) {
--dist;
next_v *= 2;
p *= 2;
if (next_v > n) {
return 0;
}
}
if (next_v + p - 1 <= n) {
return p;
} else {
return n - (next_v - 1);
}
}
ll up(ll dist, ll v, ll from)
{
if ((dist < 0)||(v < 1)) {
return 0;
}
if (dist == 0) {
if (v <= n) {
return 1;
} else {
return 0;
}
}
ll result = 0;
if (v * 2 == from) {
result += down(dist - 1, v * 2 + 1);
} else {
result += down(dist - 1, v * 2);
}
result += up(dist - 1, v / 2, v);
return result;
}
int main()
{
int t;
cin >> t;
for (int i = 0; i < t; ++i) {
ll x, k;
cin >> n >> x >> k;
cout << down(k, x) + up(k - 1, x / 2, x) << endl;
}
return 0;
}AC(Accepted=正しいプログラム)と判定されました。
Python プログラム例(ABC321E)
Python 版も基本的な考え方は同じです。
以下のプログラムは、「Python (CPython 3.11.4)」では、TLE判定となり、「Python (PyPy 3.10-v7.3.12)」で、AC判定となりました。
"""AtCoder Beginner Contest 321 E"""
def down(dist, v):
global n
if dist < 0:
return 0
if dist == 0:
if v <= n:
return 1
else:
return 0
next_v = v
p = 1
while dist > 0:
dist -= 1
next_v *= 2
p *= 2
if next_v > n:
return 0
if next_v + p - 1 <= n:
return p
else:
return n - (next_v - 1)
def up(dist, v, f):
global n
if dist < 0 or v < 1:
return 0
if dist == 0:
if v <= n:
return 1
else:
return 0
result = 0
if v * 2 == f:
result += down(dist - 1, v * 2 + 1)
else:
result += down(dist - 1, v * 2)
result += up(dist - 1, v // 2, v)
return result
t = int(input())
for i in range(t):
n, x, k = map(int, input().split())
print(down(k, x) + up(k - 1, x // 2, x))こちらも「AC」と判定されました。
最後に
この問題は、コンテストでは時間切れで取り組むことができませんでした。ただし、コンテスト後に子供側と親側に分けて考えると、AC判定を得ることができました。時間が十分にあれば解くことができた可能性があると感じました。
ABCのD問題やE問題でも解ける場合が増えてきました。解く速さを上げることにより、これらの問題に取り組む時間を増やしていきたいです。
引き続き ABC の問題を紹介していきます。