AtCoder が提供しているABC(AtCoder Beginner Contest)303 のE問題をC++とPythonで解いてみました。ABC303は、2023年5月27日21:00に実施されました。
AtCoder の紹介はこちらに、プログラミングの方針はこちらに記事があります。
E問題 Shift vs. CapsLock(Difficulty : 1113)
問題はリンク先をご覧ください。
ABC303 E問題 A Gift From the Stars
木の頂点の次数を調べることによって解くことができる問題です。AtCoder Problems による Difficulty は 1113 でした。
解答案
入力例3は頂点が多いですが、グラフは以下となります。
黄色の頂点が元の星の頂点、赤色の辺が手続きで追加された辺となります。
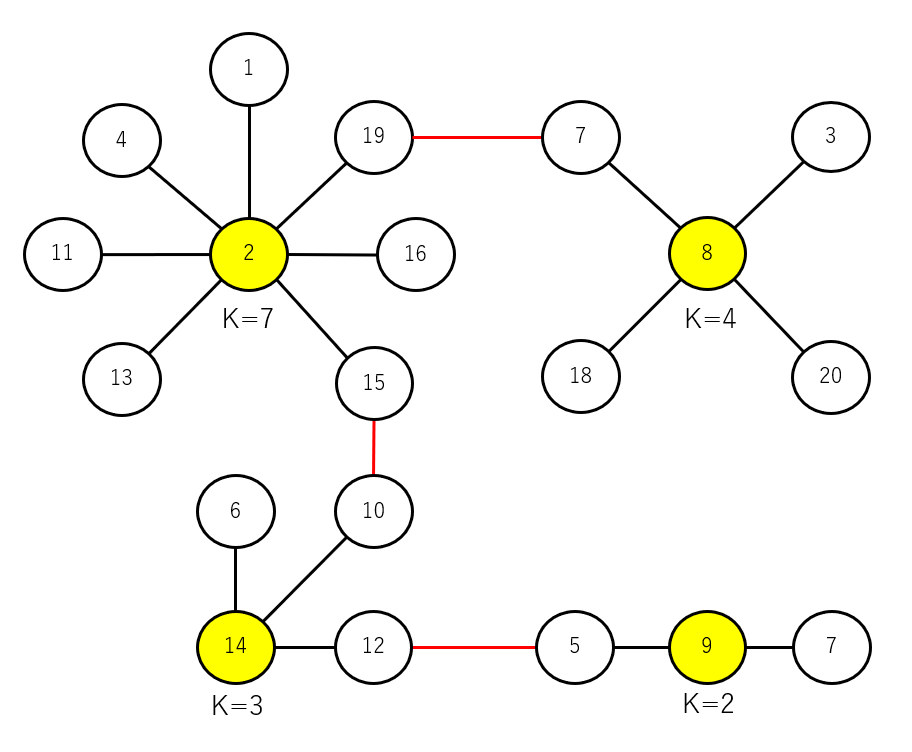
グラフを観察すると、以下が分かります。
- 次数1の頂点をつなぐため、次数3以上の頂点は元の星の頂点となる(手続きによって辺が増えない)。
- 次数 $i$ の頂点の個数を $m_i$ とすると、以下の関係が成り立つ。この式から次数2の頂点の数が分かる。
$3 \times m_2 + 4 \times m_3 + 5 \times m_4 \cdots = N$
上の例だと、$3 \times 1 + 4 \times 1 + 5\times 1 + 8 \times 1 = 20$
次数3以上の頂点の個数を求めて、計算して次数2の頂点の個数を求めることができます。
C++ プログラム例(ABC303E)
以下の手順で問題を解きます。最終的に出力する次数を配列 result に格納します。
- 各頂点の次数を配列 e[] に格納します(12、13行目)。
- 頂点の次数の頻度を map コンテナ m に格納します(18行目)
- 頂点の次数が3以上の場合
- 一時変数 temp(初期値 N)から、(次数 + 1) × 頻度を引きます(25行目)。
- 配列 result に次数を格納します(27行目)。
- temp を 3 で割った回数、result に 2 を格納します(32行目)。
- 配列 result をソートして出力します(34、37行目)。
以下が、C++プログラムとなります。
#include <bits/stdc++.h>
using namespace std;
int main()
{
int n;
cin >> n;
vector<int> e(n + 1, 0);
for (int i = 0; i < n - 1; ++i) {
int u, v;
cin >> u >> v;
++e[u];
++e[v];
}
map<int, int> m;
for (int i = 1; i <= n; ++i) {
++m[e[i]];
}
vector<int> result;
int temp = n;
for (auto e : m) {
if (e.first >= 3) {
temp -= (e.first + 1) * e.second;
for (int i = 0; i < e.second; ++i) {
result.push_back(e.first);
}
}
}
for (int i = 0; i < temp / 3; ++i) {
result.push_back(2);
}
sort(result.begin(), result.end());
for (int i = 0; i < result.size(); ++i) {
cout << result[i] << " \n"[i == result.size() - 1];
}
return 0;
}AC(Accepted=正しいプログラム)と判定されました。
Python プログラム例(ABC303E)
Python 版も C++ 版のロジックを移植しました。辞書は defaultdict を使いました(2、11行目)。Python は、リスト要素の出力が楽です(26行目)。
"""AtCoder Beginner Contest 303 E"""
from collections import defaultdict
n = int(input())
e = [0] * (n + 1)
for _ in range(n - 1):
u, v = map(int, input().split())
e[u] += 1
e[v] += 1
m = defaultdict(int)
for i in range(1, n + 1):
m[e[i]] += 1
result = []
temp = n
for k, v in m.items():
if k >= 3:
temp -= (k + 1) * v
for i in range(v):
result.append(k)
for i in range(temp // 3):
result.append(2)
result.sort()
print(*result)こちらも「AC」と判定されました。
最後に
コンテスト中は、今の自分には難しいとあきらめてしまいました。解説を読むと、頂点の次数だけで求めることができることが分かりました。新しい考え方を学べました。
引き続き ABC の問題を紹介していきます。