AtCoder が提供しているABC(AtCoder Beginner Contest)279 のD問題をC++とPythonで解いてみました。ABC279は、2022年11月26日21:00に実施されました。
AtCoder の紹介はこちらに、プログラミングの方針はこちらに記事があります。
D問題 Freefall(Difficulty : 766)
問題はリンク先をご覧ください。
微分の知識が必要な問題です。AtCoder Problems による Difficulty は、766 でした。
解答案
数学的な分析
操作を n 回行った場合、地面まで到達する時間 t は、以下となります。
$$t = B \times n + \frac{A}{\sqrt{1 + n}}$$
入力例1の場合、$A = 10$、$B = 1$ であるため、グラフは以下のようになります。出力例1の説明にあるように、自然数の範囲では、$n = 2$ のときに最小となります。
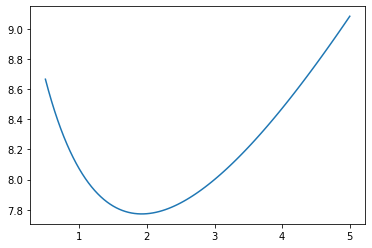
ここで、t を n で微分した $ t’ $ は以下となります。
$$t’ = B\; -\; \frac{1}{2} A \times (1 + n)^{-\frac{3}{2}}$$
$t’$ は、$n > 0$ の範囲で単調増加となります。$t’ = 0$ となる $n$ があるため、$t$ は、下に凸の関数となります。$A = 10$、$B = 1$ の場合のグラフです。$n = 2$ 付近で値が $0$ になっていることが確認できます。
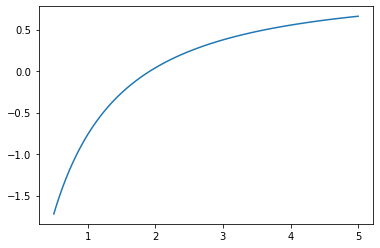
下に凸の関数なので、$t’ = 0$ となる $n$ で最小値を持ちます。その $n$ を求めます。
$$B = \frac{1}{2} A \times (1 + n)^{-\frac{3}{2}}$$
$n$ を含む項を左辺に移動して
$$(1 + n)^{\frac{3}{2}} = \frac{A}{2 \times B}$$
両辺を $2/3$ 乗して、両辺から 1 を引いて、最終的に以下を得ます。
$$n = \left( \frac{A}{2 \times B} \right)^{\frac{2}{3}}\; – \;1$$
$n$ を実数のように計算しましたが、この $n$ に近い 0 以上の整数に対して、$t$ を求めれば、それが最小値になります。
この問題は、微分に苦手意識がある人だと苦戦するかもしれません。現行の高校数学では、無理関数の微分は、数学Ⅲで履修します。
C++ プログラム例(ABC279D)
求めた計算式をプログラムに変換しました。以下がポイントです。
- n を整数化(切下げした値)した値を求める。
- power を使い累乗を求める。
- 式で求めた n が負の場合、n = 0 とする。
- n とそれより1多い値に対して落下時間を計算して、少ない方を解答とする。
- sqrt を使い平方根を求める。
- 小数点は、出力例に合わせて10桁出力する。
式を求める過程で微分が必要で難しいと感じる人がいたと思います。求めた式は短いため、プログラムは短くなります。
#include <bits/stdc++.h>
using namespace std;
typedef unsigned long long int ull;
int main()
{
ull a, b;
cin >> a >> b;
ull n = (ull)(pow((double)a / (2.0 * (double)b), 2.0/3.0) - 1.0);
if (n < 0) {
n = 0;
}
double result;
result = (double)b * n + a / sqrt(n + 1.0);
result = min(result, (double)b * (n + 1.0) + a / sqrt(n + 2.0));
printf("%.10lf\n", result);
return 0;
}このプログラムは、AC(Accepted=正しいプログラム)と判定されました。
Python プログラム例(ABC279D)
C++版を移植したプログラムが以下です。math モジュールを import して、floor と sqrt を使っています。f文字列で小数点以下10桁を出力しています。
"""AtCoder Beginner Contest 279 D"""
import math
a, b = map(int, input().split())
n = math.floor((a / (2.0 * b)) ** (2.0 / 3.0)) - 1.0
if n < 0:
n = 0
result = b * n + a / math.sqrt(n + 1.0)
result = min(result, b * (n + 1.0) + a / math.sqrt(n + 2.0))
print(f"{result:.10f}")このプログラムも「AC」と判定されました。
最後に
ABC279 は、A問題からC問題まで比較的簡単でした。一方、D問題は少し種類が異なることを問われて難易度が上がりました。
ABC を解説するのは11回となり、10回を超えました。今は、直近の問題の解説をしていますが、問題の分析も行いたいと考えています。
引き続き ABC の問題を紹介していきます。