Project Euler で紹介されている問題15を解いてみました。場合の数を考える典型問題です。大きな組み合せの数を求めることになるため、大きな整数を使える言語を採用する場合と、工夫して組込みの整数型で解答を求める方法を紹介します。
Project Euler 問題15(格子状の道)
2×2格子の左上からスタートして、右と下にしか移動できない場合、右下への経路はちょうど6通りある。
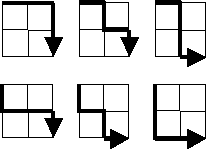
20×20の格子を通るこのような経路の通り数を求めよ。
問題文の画像は、Project Euler の画像を借用しました。
解答例
右に進むことをRと、下に進むことをDと書くと、問題文にある6通りは、以下のように表現できます(画像の順に並べています)。
RRDD RDRD RDDR
DRRD DRDR DDRR
目的地まで4つある道の選択肢の中で、右に進む2つを選ぶ通り数と同じとなります。これは、組み合せの数と呼ばれており、4個のものから2個を選ぶ通り数を $_4C_2$ と書きます。具体的な計算は以下となります。
$$ _4C_2 = \frac{4 \times 3}{2 \times 1} = 6$$
解きたい問題は、目的地まで40ある道(20 + 20)の選択肢の中で、右に進む20を選ぶ通り数と同じになります。つまり $_{40}C_{20}$ を求める問題になります。求めたい数は以下となります。
$$ _{40}C_{20} = \frac{40 \times 39 \times … \times 22 \times 21}{20 \times 10 \times … \times 2 \times 1} $$
この数は、表記の見た目より大きくなります。分子は30桁の数で、分母は19桁の数となります。
整数の長さに制約がない Python で実装してみます。Python 3.8 から、math モジュールに組み合せの数を計算する comb 関数が追加されましたので、これを使います。
"""Project Euler Problem015"""
import math
print("Problem015: " + str(math.comb(40, 20)))やはり Python は楽ですね。
問題13で導入した GMP ライブラリを使って、C言語でも記述しました。GMP にも組み合せの数を求める関数 mpz_bin_uiui があるため、これを使います。
#include <stdio.h>
#include <gmp.h>
int main(void)
{
mpz_t n;
mpz_init(n);
mpz_bin_uiui(n, 40, 20);
gmp_printf("Problem015: %Zd\n", n);
mpz_clear(n);
return 0;
}GMP ライブライを使っているため、コンパイル時(リンク時)には、「-lgmp」オプションが必要となります。また多くのオンライン実行環境では、コンパイルできません。
解答例(64ビット整数でやりきる)
求めたい組み合せの数は、以下です。
$$ _{40}C_{20} = \frac{40 \times 39 \times … \times 22 \times 21}{20 \times 10 \times … \times 2 \times 1} $$
分子が30桁で、分母が19桁と大きな数になりますが、組み合せの数なので、分母は分子で割り切れます。分子で掛ける数と分母で掛ける数をひとつづつ増やしていき、分子と分母の最大公約数で分子と分母を割っていけば、桁あふれすることなく計算ができます。最大公約数で割っていくと、分母は最終的に1になります。
このアイデアで実装したのが以下です。最大公約数を求める関数 gcd は、問題5で使った関数を再流用します。
#include <stdio.h>
typedef unsigned long long ull;
ull gcd(ull a, ull b)
{
if (b == 0) {
return a;
} else {
return gcd(b, a % b);
}
}
int main(void)
{
int i;
ull a = 40;
ull b = 20;
ull g;
for (i = 1; i <= 19; ++i) {
a *= (ull)(40 - i);
b *= (ull)(20 - i);
g = gcd(a, b);
a = a / g;
b = b / g;
}
printf("Problem015: %lld\n", a);
return 0;
}桁あふれを起こすことなく、無事に解答を求めることができました。
最後に
格子状の道の最短経路の通り数を求めるのは、高校数学で履修する数学A 「場合の数と確率」の定番演習となっています。高校数学の三大網羅系参考書を調べてみました(買った時期がばらばらなのはご容赦ください)。
- 青チャート(基礎からの数学A)数研出版 2019年2月増補改訂版
例題31 - Focus Gold 数学Ⅰ+A 啓林館 2012年3月
例題189 - New Action LEGEND 数学Ⅰ+A 東京書籍 2018年9月
例題194
Project Euler は、純粋に数学、もしくはプログラミングとして興味深い題材を取り上げていると考えています。その題材の多くは学校教育で履修する範囲に入っているため、学び直したいかたは、学生の参考書を使うことも視野に入れてはどうでしょうか。
引き続き、Project Euler の問題を紹介していきます。







