AtCoder が提供しているABC(AtCoder Beginner Contest)354 D問題をC++とPythonで解いてみました。ABC354は、2024年5月18日21:00に実施されました。
AtCoder の紹介はこちらに、プログラミングの方針はこちらに記事があります。
D問題 AtCoder Wallpaper(Difficulty : 1259)
問題の詳細は、リンク先をご覧ください。
2次元累積和で解くことができます。AtCoder Problems による Difficulty は 1259 でした。
解答案
ABC331 D問題(解説記事)とほぼ同じ問題です。同じパターンが繰り返されるため、原点を左下とする関数を作るとプログラムがすっきりと書けます。
今回の問題は、4×2の赤枠で示したパターンが繰り返されます。
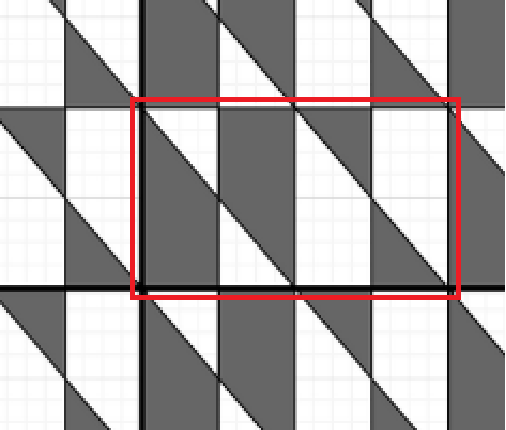
この赤枠の2次元累積和を計算します。この部分の面積を配列で表現すると以下になります。注)上下が逆になっているように見えます。値は2倍しています。
{{2, 1, 0, 1},
{1, 2, 1, 0,}};この面積の2次元累積和を求めると以下の配列となります。横方向にも縦方向にも配列をひとつ余分に取っています。
int s[3][5] = {
{0, 0, 0, 0, 0},
{0, 2, 3, 3, 4},
{0, 3, 6, 7, 8}};この2次元累積和を使うと、原点を左下とする長方形の黒い部分の面積が簡単に求まります。ABC331 D問題の公式解説の図で説明します。
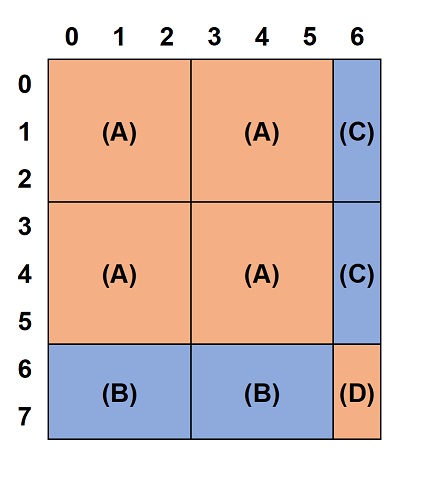
この長方形に含まれる黒の面積は以下の関数 black で求めることができます。問題では、左下(0,0) から 右上 (i, j) に含まれる黒の面積となります。
typedef long long int ll;
ll black(ll i, ll j)
{
ll result = 0;
ll all = s[2][4]; // Aの面積
ll ni = i / 4;
ll nj = j / 2;
result += all * ni * nj; // Aの面積×含まれている個数
ll mi = i % 4;
ll mj = j % 2;
result += s[mj][4] * ni; // Bの面積×Bの個数
result += s[2][mi] * nj; // Cの面積×Cの個数
result += s[mj][mi]; // Dの面積を加える。
return result;
}C++ プログラム例(ABC354D)
この問題は、負の数が頂点になると計算が煩雑になるため、$x$ と $y$ に $10^9$ を加えておきます。$10^9$ は、2でも4でも割り切れるため、面積は変わりません。
上で説明した関数 black を使うと、以下の式で面積を求めることができます。
black(c, d) – black(a, d) – black(c, b) + black(a, b)
以下が、C++プログラムです。
#include <bits/stdc++.h>
using namespace std;
typedef long long int ll;
#define OFFSET 1000000000LL;
int s[3][5] = {{0, 0, 0, 0, 0}, {0, 2, 3, 3, 4}, {0, 3, 6, 7, 8}};
ll black(ll i, ll j)
{
ll result = 0;
ll all = s[2][4];
ll ni = i / 4;
ll nj = j / 2;
result += all * ni * nj;
ll mi = i % 4;
ll mj = j % 2;
result += s[mj][4] * ni;
result += s[2][mi] * nj;
result += s[mj][mi];
return result;
}
int main()
{
ll a, b, c, d;
cin >> a >> b >> c >> d;
a += OFFSET;
b += OFFSET;
c += OFFSET;
d += OFFSET;
cout << black(c, d) - black(a, d) - black(c, b) + black(a, b) << endl;
return 0;
}AC(Accepted=正しいプログラム)と判定されました。
Python プログラム例(ABC354D)
Python版も基本的な考え方は同じです。以下がプログラムです。
"""AtCoder Beginner Contest 354 D"""
OFFSET = 10 ** 9
s = [[0, 0, 0, 0, 0], [0, 2, 3, 3, 4], [0, 3, 6, 7, 8]]
def black(i, j):
global s
result = 0
all_b = s[2][4]
ni = i // 4
nj = j // 2
result += all_b * ni * nj
mi = i % 4
mj = j % 2
result += s[mj][4] * ni
result += s[2][mi] * nj
result += s[mj][mi]
return result
a, b, c, d = map(int, input().split())
a += OFFSET
b += OFFSET
c += OFFSET
d += OFFSET
print(black(c, d) - black(a, d) - black(c, b) + black(a, b))こちらも「AC」と判定されました。
最後に
ABC331問題を解説する記事では、「次に見たときに解けるようになればと思います」と書いていました。似た問題をコンテストで解くことができました。私にとって、Diff 1259 は、コンテストで解けた問題の最高難易度でした。
引き続き ABC の問題を紹介していきます。