AtCoder が提供しているABC(AtCoder Beginner Contest)340 のD問題をC++とPythonで解いてみました。ABC340は、2024年2月10日21:00に実施されました。
AtCoder の紹介はこちらに、プログラミングの方針はこちらに記事があります。
D問題 Divide and Divide(Difficulty : 784)
問題はリンク先をご覧ください。
有向グラフの最短経路を求める問題と考えることができます。AtCoder Problems による Difficulty は 784 でした。
解答案
入力例1を図示します。赤い線の経路が最短となります(350秒)。
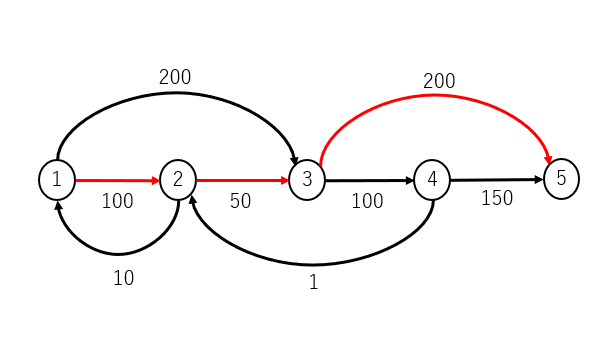
全体を有向グラフと考えて、頂点1から頂点Nまでの最短経路を求める問題に帰着できます。ダイクストラ法を適用します。
C++ プログラム例(ABC340D)
この問題はグラフの辺を設定する25、26行目がポイントで、残りのコードは定番コードです。この問題は、各頂点で $A_i$ 秒掛ければ、次の頂点に行くため、頂点1から頂点Nには、必ず到達します。このため、距離が無限大(INF)になる特別な処理は必要ありません。
以下が、C++プログラムとなります。
#include <bits/stdc++.h>
using namespace std;
typedef long long int ll;
#define INF (1LL << 60)
typedef pair<ll, int> P;
struct Edge {
int to;
ll weight;
Edge() { }
Edge(int t, ll w) : to(t), weight(w) { }
};
int main()
{
int n;
cin >> n;
vector<vector<Edge>> G(n + 1);
vector<ll> a(n);
vector<ll> b(n);
vector<int> x(n);
for (int i = 1; i < n; ++i) {
cin >> a[i] >> b[i] >> x[i];
G[i].push_back(Edge(i + 1, a[i]));
G[i].push_back(Edge(x[i], b[i]));
}
vector<ll> dist(n + 1, INF);
priority_queue<P, vector<P>, greater<P>> que;
dist[1] = 0;
que.push(P(0, 1));
while (!que.empty()) {
P p = que.top();
que.pop();
int now = p.second;
if (dist[now] < p.first) {
continue;
}
for (auto next_v : G[now]) {
if (dist[next_v.to] > dist[now] + next_v.weight) {
dist[next_v.to] = dist[now] + next_v.weight;
que.push(P(dist[next_v.to], next_v.to));
}
}
}
cout << dist[n] << endl;
return 0;
}AC(Accepted=正しいプログラム)と判定されました。
Python プログラム例(ABC340D)
Python 版も基本的な考え方は同じです。以下となります。
"""AtCoder Beginner Contest 340 D"""
import heapq
INF = 1 << 60
n = int(input())
G = [[] for i in range(n + 1)]
for i in range(1, n):
a, b, x = map(int, input().split())
G[i].append((i + 1, a))
G[i].append((x, b))
que = []
heapq.heapify(que)
dist = [INF] * (n + 1)
dist[1] = 0
heapq.heappush(que, (0, 1))
while que:
p = heapq.heappop(que)
now = p[1]
if dist[now] < p[0]:
continue
for next_v in G[now]:
if dist[next_v[0]] > dist[now] + next_v[1]:
dist[next_v[0]] = dist[now] + next_v[1]
heapq.heappush(que, (dist[next_v[0]], next_v[0]))
print(dist[n])こちらも「AC」と判定されました。
最後に
コンテストでは、最初DPでプログラムを書きましたが、入力例2を確認して、グラフを適用する問題と気づきました。ダイクストラ法は、コードを整備していたため早くプログラムを書くことができました。
引き続き ABC の問題を紹介していきます。