AtCoder が提供しているABC(AtCoder Beginner Contest)338 のE問題をC++とPythonで解いてみました。ABC338は、2024年1月27日21:00に実施されました。
AtCoder の紹介はこちらに、プログラミングの方針はこちらに記事があります。
E問題 Chords(Difficulty : 1220)
問題はリンク先をご覧ください。
スタックを使えば、すっきりとしたプログラムになります。AtCoder Problems による Difficulty は 1220 でした。
解答案
公式解説を参考にしました。
$A_i < B_i$ となるように $A_i$ と $B_i$ を入れ替えても一般性を失いません。この入れ替えにより、$2N$ と $1$ をまたぐ弦はないと考えることができます。以下の図のように $1$ と $2N$ の間で切り開いて直線にします。この図も公式解説から引用させていただきました。
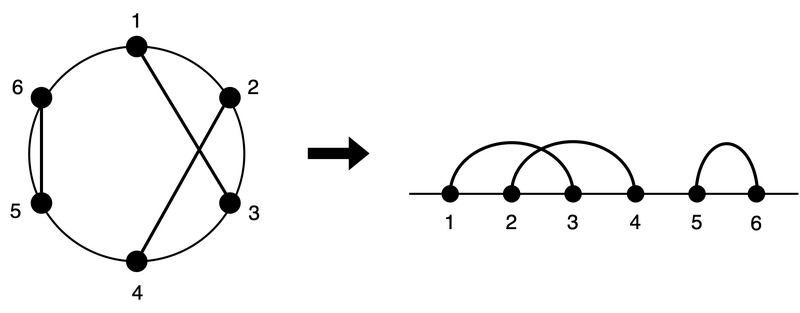
右の図にように開くと、$A_i$ となる場合は、スタックに $i$ の値を push して、$B_j$ となる場合は、スタックから pop した値が、組となっている $A_i$ か調べます。ひとつでも組になっていない値が pop された場合は、交点を持つことになります。
C++ プログラム例(ABC338E)
上記の手順をプログラムとして実装します。
- $A_i$ の位置を set コンテナ a に格納します(17行目)。
- $B_i$ の位置を set コンテナ b に格納します(18行目)。
- $B_i$ をキー、$A_i$ をバリューとする map コンテナ b2a に格納します(19行目)。
- $1$ から $2N$ まで以下の操作を行います。
- その位置が、$A_i$ なら、$i$ の値をスタックに push する(26行目)。
- その位置が、$B_i$ なら、スタック一番上の値を取得して、b2a[i] と比較する。一致していなければ、交点を持ち、ループから抜ける。
- 最後まで走査できれば、交点を持たない。
- 値を出力する(result の値が逆になっていることに注意)。
以下が、C++プログラムとなります。
#include <bits/stdc++.h>
using namespace std;
int main()
{
int n;
cin >> n;
set<int> a;
set<int> b;
map<int, int> b2a;
for (int i = 0; i < n; ++i) {
int t_a, t_b;
cin >> t_a >> t_b;
if (t_a > t_b) {
swap(t_a, t_b);
}
a.insert(t_a);
b.insert(t_b);
b2a[t_b] = t_a;
}
bool result = true;
vector<int> st;
for (int i = 1; i <= 2 * n; ++i) {
if (a.find(i) != a.end()) {
st.push_back(i);
} else if (b.find(i) != b.end()) {
if (b2a[i] != st.back()) {
result = false;
break;
} else {
st.pop_back();
}
}
}
if (!result) {
cout << "Yes" << endl;
} else {
cout << "No" << endl;
}
return 0;
}AC(Accepted=正しいプログラム)と判定されました。
Python プログラム例(ABC338E)
Python 版も基本的な考え方は同じです。以下となります。
"""AtCoder Beginner Contest 338 E"""
n = int(input())
a = set()
b = set()
b2a = {}
for i in range(n):
t_a, t_b = map(int, input().split())
if t_a > t_b:
t_a, t_b = t_b, t_a
a.add(t_a)
b.add(t_b)
b2a[t_b] = t_a
result = True
st = []
for i in range(1, 2 * n + 1):
if i in a:
st.append(i)
elif i in b:
if b2a[i] != st.pop():
result = False
break
print("Yes" if not result else "No")こちらも「AC」と判定されました。
最後に
このE問題は、すべての弦が隣接している場合や、すべての弦が平行になる場合、それを組み合わせる場合などの実装を試しましたが、WAが取れませんでした。
公式解説を参照して、その解き方に感心しました。たいへん勉強になりました。
引き続き ABC の問題を紹介していきます。