AtCoder が提供しているABC(AtCoder Beginner Contest)335 のE問題をC++で解いてみました。ABC335は、2024年1月6日21:00に実施されました。
AtCoder の紹介はこちらに、プログラミングの方針はこちらに記事があります。
E問題 Non-Decreasing Colorful Path(Difficulty : 1540)
問題はリンク先をご覧ください。
ABC335 E問題 Non-Decreasing Colorful Path
同じ整数を持つ頂点を同一視すると、DPで解けます。AtCoder Problems による Difficulty は 1540 でした。
解答案
単純パスをすべて求める方法は時間が足りない。
最初に、すべての単純パスを求めて、パスに含まれている整数の種類の最大値を求めます。グラフの定番コードが多くを占めます。
- 関数 dfs で、単純パスを求めます。
- 終点までたどり着いた場合に、格納している path に含まれている頂点の整数を set コンテナ num に格納して、最大値を更新します(15ー24)。
#include <bits/stdc++.h>
using namespace std;
vector<vector<int>> G;
vector<bool> seen;
vector<int> point;
vector<int> path;
int result = 0;
void dfs(int v, int g)
{
seen[v] = true;
path.push_back(v);
if (v == g) {
set<int> num;
for (auto e : path) {
num.insert(point[e]);
}
result = max(result, (int)num.size());
path.pop_back();
seen[v] = false;
return;
}
for (auto next_v : G[v]) {
if ((!seen[next_v])&&(point[v]) <= point[next_v]) {
dfs(next_v, g);
}
}
path.pop_back();
seen[v] = false;
}
int main()
{
int n, m;
cin >> n >> m;
point.resize(n + 1, 0);
for (int i = 1; i <= n; ++i) {
cin >> point[i];
}
G.resize(n + 1);
seen.assign(n + 1, false);
for (int i = 0; i < m; ++i) {
int u, v;
cin >> u >> v;
G[u].push_back(v);
G[v].push_back(u);
}
dfs(1, n);
cout << result << endl;
return 0;
}このプログラムは、正解となるテストケースもありますが、半数以上のテストケースで TLE(Time Limit Exceeded)と判定されました。頂点と辺によっては、単純パスが非常に多くあるため、時間が足らなくなります。
- 関数 dfs で次の頂点を調べる26行目で、頂点が持つ整数を確認していますが、確認することによるコストが発生しています。
- すべての単純パスを求めるため、一度訪れた頂点も抜けるときに、「訪れなかった」ことにしています。これは、関数 dfs の seen[v] の処理をご覧ください。
閉路がない有向グラフ(DAG: Directed acyclic graph)と考える
無向グラフとして処理することは計算量的に難しいようです。
全体を閉路がない有向グラフにできないか考えてみます。入力例3のグラフを可視化してみました。頂点が持つ数字を小さい方から大きい方に向きを付けました。数字が同じ場合は、(恣意的ですが)頂点番号の順に向きを付けました(この例では、うまく行きます)。
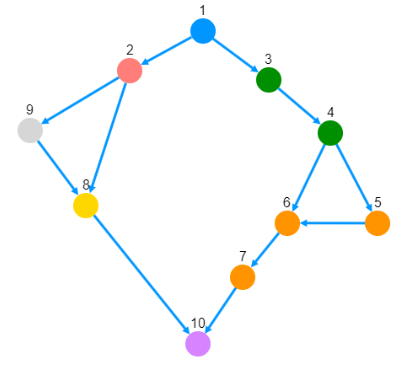
ツールは、グラフ可視化ツールを使いました。
このグラフでは、頂点1→頂点10で右側の経路の方が多くの頂点を経由しますが、左側の経路の方が多くの整数を通ります。解答は、1→2→9→8→10の5となります。
以下のように考えます。
- 頂点の整数は、小さい方からより大きい方にしか移動できなため、移動できる方向に向きを設定する。
- 同じ整数を持つ頂点が連結している場合は、同一視する。
これにより、グラフ全体を閉路がない有向グラフと考えることができます。DP で頂点1から頂点Nまでのもっとも長いパスを求めることができます。
C++ プログラム例(ABC335E)
プログラムを補足します。
- 頂点の数字の最大値を max_a として計算しておきます(16行目)。
- 頂点の数字は、1からNではなく、0からN-1とします。これにより、頂点 u が持つ整数を a[u] で参照することができます。
- UnionFind を使って頂点を管理します。同じ数字を持ち連結している頂点を同一視します(30行目の merge 呼び出し)。
- 頂点を u ではなく、uf.leader(u) でアクセスします。
- UnionFind は、AtCoder Library を使いました。
- 頂点の数字を添え字にして、頂点の遷移 u → v の組を vp として格納します(32行目)。
- dp[v] を頂点0から頂点vへのパスにおける、最高得点とします。
- dp[0] = 1 として、それ以外はマイナス無限大の値を設定しておきます。
- 頂点が持つ値が小さい順に、dp[v] を(大きくなる場合) dp[u] + 1 で更新します。
- dp[n-1] が求める解になります。正の値でなければ、到達しません。
以下が、C++プログラムとなります。
#include <bits/stdc++.h>
#include <atcoder/dsu>
using namespace std;
using namespace atcoder;
#define INF (1 << 30)
int main()
{
int n, m;
cin >> n >> m;
vector<int> a(n);
int max_a = 0;
for (int i = 0; i < n; ++i) {
cin >> a[i];
max_a = max(max_a, a[i]);
}
dsu uf(n);
vector<vector<pair<int, int>>> vp(max_a + 1);
for (int i = 0; i < m; ++i) {
int u, v;
cin >> u >> v;
--u;
--v;
if (a[u] > a[v]) {
swap(u, v);
}
if (a[u] == a[v]) {
uf.merge(u, v);
} else {
vp[a[u]].push_back(make_pair(u, v));
}
}
vector<int> dp(n, -INF);
dp[uf.leader(0)] = 1;
for (int i = 1; i <= max_a; ++i) {
for (auto e : vp[i]) {
int u = uf.leader(e.first);
int v = uf.leader(e.second);
if (dp[u] > 0) {
dp[v] = max(dp[v], dp[u] + 1);
}
}
}
cout << max(0, dp[uf.leader(n - 1)]) << endl;
return 0;
}AC(Accepted=正しいプログラム)と判定されました。
Python のUnionFindについて
Python は、UnionFind を標準ライブラリとしては用意していません。このブログの Python プログラムは、なるべく言語標準のライブラリで実装したいと考えています。このような事情で、この記事では、Python に移植したプログラムの紹介を省略します。
最後に
コンテストでは、DFS で単純パスをすべて求めるプログラムを提出しました。TLE 判定となりました。頂点が持つ整数を小さい方から処理するアイデアは気が付きましたが、時間内に実装ができませんでした。
コンテスト後に、公式解説で理解したことを記事にしました。学ぶことができました。
引き続き ABC の問題を紹介していきます。