AtCoder が提供しているABC(AtCoder Beginner Contest)311 のC問題をC++とPythonで解いてみました。ABC311は、2023年7月22日21:00に実施されました。
AtCoder の紹介はこちらに、プログラミングの方針はこちらに記事があります。
C問題 Find it!(Difficulty : 448)
問題はリンク先をご覧ください。
有向グラフの閉路を求める問題です。AtCoder Problems による Difficulty は 448 でした。
解答案
グラフの閉路を求める問題としては、ABC285D(解説記事)、ABC288C(解説記事)がありました。同じ考え方で解いてみます。
グラフは、DFS(深さ優先探索:Depth-First Search)で探索します。「訪れたか」を表す bool 型の seen に「訪れきったか」を表す finished を加えました。seen が true で、finished が false であれば、閉路を検出したことになります。
C++ プログラム例(ABC311C)
DFS を使って閉路を求める
今回の問題は、閉路に含まれる頂点を出力する必要があります。
関数 dfs で、頂点を配列 result に push_back します(19行目)。閉路を検出したら、is_detect を true に変更します。合わせて閉路の開始となる点を end_v として記憶します(22-25行目)。
閉路ではない場合は、配列 result から pop_back します(34行目)。
入力例3のグラフは以下となります(この画像は問題から借用しました)。
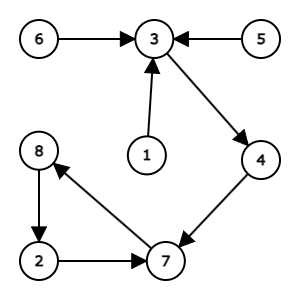
このグラフのように閉路を持つグラフでも始点から閉路になるわけではありません。このため、閉路が始まる点(end_v)から頂点を出力しています(58ー63、66行目)。
以下が、C++プログラムとなります。
#include <bits/stdc++.h>
using namespace std;
vector<vector<int>> G;
vector<bool> seen;
vector<bool> finished;
bool is_detect = false;
vector<int> result;
int end_v;
void dfs(int v)
{
if (is_detect) {
return;
}
seen[v] = true;
result.push_back(v);
for (auto next_v : G[v]) {
if (seen[next_v]) {
if (!finished[next_v]) {
is_detect = true;
end_v = next_v;
}
} else {
dfs(next_v);
}
}
if (!is_detect) {
result.pop_back();
}
finished[v] = true;
}
int main()
{
int n;
cin >> n;
G.resize(n + 1);
seen.assign(n + 1, false);
finished.assign(n + 1, false);
for (int i = 0; i < n; ++i) {
int a;
cin >> a;
G[i + 1].push_back(a);
}
for (int i = 0; i < n; ++i) {
dfs(i);
if (is_detect) {
break;
}
}
int start_index = -1;
for (int i = 0; i < result.size(); ++i) {
if (result[i] == end_v) {
start_index = i;
}
}
cout << result.size() - start_index << endl;
for (int i = start_index; i < result.size(); ++i) {
cout << result[i] << " ";
}
cout << endl;
return 0;
}Functional graph であることを使って求める
一方、制約から各頂点はその頂点を始点とする辺を1つ持ちます(このようなグラフを functional graph と呼ぶようです)。この場合、どの頂点から始めても、辺をある回数たどると、閉路にたどり着きます(入力例3のグラフをご覧ください)。
この問題の場合、どの頂点から始めても頂点の数 N 回、辺をたどる(13ー16行目)ことにより閉路にたどり着きます。どの頂点でもよいため頂点1としました。閉路内であれば、一周するまで頂点を配列 result に格納して、出力するだけです。前述のプログラムより簡単に書けています。
#include <bits/stdc++.h>
using namespace std;
int main()
{
int n;
cin >> n;
vector<int> next(n + 1);
for (int i = 1; i <= n; ++i) {
cin >> next[i];
}
int start_v = 1;
for (int i = 0; i < n; ++i) {
start_v = next[start_v];
}
vector<int> result;
int now = start_v;
result.push_back(now);
while (next[now] != start_v) {
now = next[now];
result.push_back(now);
}
cout << result.size() << endl;
for (int i = 0; i < result.size(); ++i) {
cout << result[i] << " \n"[i == result.size() - 1];
}
return 0;
}どちらも AC(Accepted=正しいプログラム)と判定されました。
Python プログラム例(ABC311C)
C++ の後者の例を移植しました。リストの添え字が 0 から始まるため、ひとつ要素を挿入しています(4行目)。また next は、Python の組込み関数の名前と一致しているため変数名を next_v に変更しています。
"""AtCoder Beginner Contest 311 C"""
n = int(input())
next_v = list(map(int, input().split()))
next_v.insert(0, 0)
start_v = 1
for i in range(n):
start_v = next_v[start_v]
result = []
now = start_v
result.append(now)
while next_v[now] != start_v:
now = next_v[now]
result.append(now)
print(len(result))
print(*result)こちらも「AC」と判定されました。
最後に
閉路を求める問題となっていたため、慣れている DFS を使って解きました。公式解説に併記されているユーザ解説によって、もっと簡単に解けることが分かったため、そのプログラムも紹介しました。Funcional graph という概念を学べました。
引き続き ABC の問題を紹介していきます。