AtCoder が提供しているABC(AtCoder Beginner Contest)274 のD問題をC++で解いてみました。ABC274は、2022年10月22日21:00に実施されました。
AtCoder の紹介はこちらに、プログラミングの方針はこちらに記事があります。
D問題 Robot Arms 2(Difficulty : 916)
問題はリンク先をご覧ください。
DP(動的計画法)を使う問題です。AtCoder Problems による Difficulty は、916 でした。
解答案
DP(Dynamic Programming: 動的計画法)の紹介
DP は、問題を漸化式でモデリングします。今回、仮に問題を一次元(x軸だけで考える)としましょう。
- 正の整数列 A1、A2、A3、…、An が与えられる。
- p1 = (0, 0) とする。
- p2 = (A1, 0) とする。
- p3 = (A1 – A2, 0) もしくは (A1 + A2, 0) となる。
ここで、dpx[n][x] を pn が座標 x になる可能性があれば true、可能性がなければ false になる bool 型の配列とします。
- dpx[1][0] = true、それ以外の dpx[1][x] = false
- dpx[2][A1] = true、それ以外の dpx[2][x] = false
- dpx[i][x] = dpx[i-1][x – Ai-1] or dpx[i-1][x + Ai-1]
で計算していけば、dpx[n+1][x] の値から解答を出力することができます。
ここで、問題が求めている2次元に話を戻します。入力例1は以下となります。
- A1 = 2、A2 = 1、A3 = 3
- p4 が (-1, 1) になるか?
答えは ”Yes” となります。図示すれば以下となります(この図は、問題から借用しました。)。
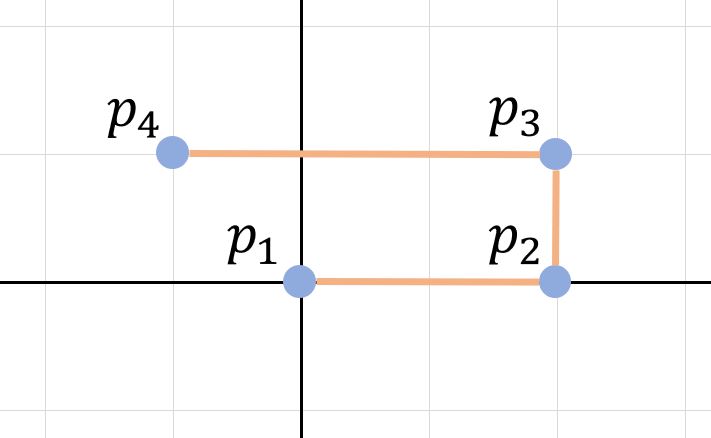
ここで、2次元になっていますが、pn に移るとき、n が偶数なら x しか変動せず、n が奇数なら、y しか変動しないことが分かります。
- dpx[n][x] を pn が座標 x になる可能性があれば true、可能性がなければ false になる bool 型の配列とします。
- dpy[n][y] を pn が座標 y になる可能性があれば true、可能性がなければ false になる bool 型の配列とします。
ここで、dpx[n][x] について、以下の初期値、および漸化式が成立します。
- dpx[1][0] = true、それ以外は false
- dpx[2][A1] = true、それ以外は false
- i が偶数の場合
- dpx[i][x] = dpx[i-1][x – Ai-1] or dpx[i-1][x + Ai-1]
- i が奇数の場合(x の値が変わらない)
- dpx[i][x] = dpx[i-1][x]
dpy[n][y] も同じ考え方で、漸化式を求めることができます。
最終的に dpx[n+1][x] と dpy[n+1][y] が共に true であれば、解答が “Yes”、それ以外の場合は、”No” となります。
C++ プログラム例(ABC274D)
漸化式をプログラムに落とし込みました。問題には以下の制約があります。
- $2 \leqq N \leqq 10^3$
- $1 \leqq A_i \leqq 10$
これから、$|x|, |y| \leqq 10^4$ となります。このため、配列では、104 をオフセットして加えて -104 から 104 までの値を表現できるようにします。
#define OFFSET 10000
bool dpx[1002][2 * OFFSET + 1];
bool dpy[1002][2 * OFFSET + 1];pn+1 まで求めるため、最初の添え字は、1002(1001+1)としています。
また、Ai は、問題文では、1 オリジンですが、プログラムの扱いやすさから 0 オリジンにしています。
dpx に対して行う演算だけを抽出すると以下のようになります。上の漸化式と比較してください。
dpx[1][0 + OFFSET] = true;
dpx[2][a[0] + OFFSET] = true;
for (int i = 3; i <= n + 1; ++i) {
for (int j = -OFFSET; j <= OFFSET; ++j) {
if (i % 2 == 0) {
dpx[i][j + OFFSET] = dpx[i-1][j + a[i-2] + OFFSET]
|| dpx[i-1][j - a[i-2] + OFFSET];
} else {
dpx[i][j + OFFSET] = dpx[i-1][j + OFFSET];
}
}
}ただし、上のコードは配列の範囲外にアクセスする可能性があります。配列外アクセスしないように条件を加える必要があります。
dpyの処理も含む最終的な C++ のプログラムは、以下となります。
#include <bits/stdc++.h>
using namespace std;
#define OFFSET 10000
bool dpx[1002][2 * OFFSET + 1];
bool dpy[1002][2 * OFFSET + 1];
int main()
{
int n, x, y;
cin >> n >> x >> y;
vector<int> a(n);
for (int i = 0; i < n; ++i) {
cin >> a[i];
}
dpx[1][0 + OFFSET] = true;
dpx[2][a[0] + OFFSET] = true;
dpy[1][0 + OFFSET] = true;
dpy[2][0 + OFFSET] = true;
for (int i = 3; i <= n + 1; ++i) {
for (int j = -OFFSET; j <= OFFSET; ++j) {
if (i % 2 == 0) {
if (j - a[i-2] + OFFSET < 0) {
dpx[i][j + OFFSET] = dpx[i-1][j + a[i-2] + OFFSET];
} else if (2 * OFFSET + 1 <= j + a[i-2] + OFFSET) {
dpx[i][j + OFFSET] = dpx[i-1][j - a[i-2] + OFFSET];
} else {
dpx[i][j + OFFSET] = dpx[i-1][j + a[i-2] + OFFSET]
|| dpx[i-1][j - a[i-2] + OFFSET];
}
dpy[i][j + OFFSET] = dpy[i-1][j + OFFSET];
} else {
dpx[i][j + OFFSET] = dpx[i-1][j + OFFSET];
if (j - a[i-2] + OFFSET < 0) {
dpy[i][j + OFFSET] = dpy[i-1][j + a[i-2] + OFFSET];
} else if (2 * OFFSET + 1 <= j + a[i-2] + OFFSET) {
dpy[i][j + OFFSET] = dpy[i-1][j - a[i-2] + OFFSET];
} else {
dpy[i][j + OFFSET] = dpy[i-1][j + a[i-2] + OFFSET]
|| dpy[i-1][j - a[i-2] + OFFSET];
}
}
}
}
if (dpx[n+1][x + OFFSET] && dpy[n+1][y + OFFSET]) {
cout << "Yes" << endl;
} else {
cout << "No" << endl;
}
return 0;
}AC(Accepted=正しいプログラム)と判定されました。
今回は、かなり記事が長くなりました。Python でのプログラム紹介は省略します。
最後に
D問題では、DPを使う問題が数多く見られました。このため、DP の解説に挑戦しました。
今回の問題では、プログラムでの表現には、オフセットや、配列外アクセスを避けるための条件判断が含まれているためコードが煩雑に見えます。ただ、本質は漸化式を求めて、それに従い計算することが中心になります。
引き続き ABC の問題を紹介していきます。